字符串匹配-KMP - SixTeenBlog

##KMP如何移动

KMP相对于传统的BF算法，改进了字符串移动的规则，传统的BF字符匹配算法没用充分利用到已经匹配过的字符的信息，每次只移动一位，因此效率不高，而KMP引入一个next数组(有效的前缀)，充分利用匹配过的信息，加快了移动的效率(增加了移动的距离)。

举个例子：

target string：ABCDAB-ABCDABCDABDE
pattern string：ABCDABD

pattern的next数组：

KMP-0

开始匹配：

第一次匹配到’-‘和’D’不匹配,根据next数组和最后一个匹配成功的字符,

ABCDAB-ABCDABCDABDE
ABCDABD

pattern右移:

已经匹配的字符数-next数组的值

这样移动可以让已经匹配过的target的后缀对齐pattern的前缀，所以6-2=4，右移4位，前缀AB对齐已匹配的后缀AB

ABCDAB-ABCDABCDABDE
    ABCDABD

’-‘和’C’不匹配，同理，右移2-0=2

ABCDAB-ABCDABCDABDE
      ABCDABD

一开始就不匹配，右移一位

ABCDAB-ABCDABCDABDE
       ABCDABD

‘D’和’C’不匹配，6-2=4

ABCDAB-ABCDABCDABDE
           ABCDABD

匹配成功。

##获取next数组以模式串AGCTAGCAGCTAGCTG为例

KMP-1

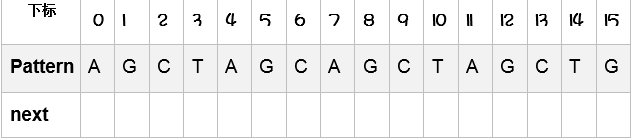
第一个前面没有字符，所以与前缀匹配的长度肯定是0 KMP-2

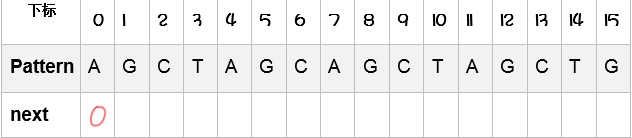
因为’G’!=’A’,所以G位置的next数组也是0，同理，C，T位置的next数组的值也是0 KMP-3

‘A’==’A’,说明这个位置存在一个字符与模式串的前缀匹配，且长度是1 KMP-4

每正确匹配一个，长度都加1 KMP-5

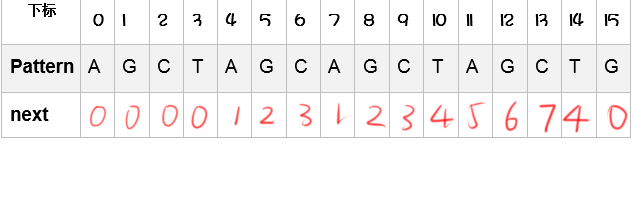
到了第7位A的时候，没有与第三位的T匹配，现在已经匹配的前缀是AGC，任意子后缀和A组成的前缀(GCA,CA)都不能匹配模式串的前缀，因此，我们从这个位置从头开始匹配

KMP-6

我们又再次匹配失败，这时，已经匹配的前缀是 AGCCTAGC,任意子后缀和T组成的前缀中，AGCT是能匹配模式串前缀的一个最长串，所以，T处的next值是4，同理可得G处是0 KMP-7

void setNextarray(){
    nextarray[0] = 0;
    int k = 0;
    int len = strlen(pattern);
    //给pattern的每一位对应的next数组赋值
    for (int i = 1; i < len; i++){
        k = nextarray[i-1];
        //先比较现在i位的是否和k位的相等，如果不等且k不是指向第一位数，那么
        //k-1对应的是pattern[i-1]之前对应的一位的下标，nextarray[k-1]就是上一层对应的结尾
        while (pattern[i] != pattern[k] && k != 0){
            k = nextarray[k - 1];
        }
        //如果成功匹配，赋值k+1
        if (pattern[i] == pattern[k]){
            nextarray[i] = k + 1;
        }
        //否则从头开始匹配
        else{
            nextarray[i] = 0;
        }
    }
}

##KMP算法

#include<iostream>
#include<string.h>
using namespace std;

int nextarray[1000000];
char pattern[1000000];
char target[1000000];

void setNextarray(){
    nextarray[0] = 0;
    int k = 0;
    int len = strlen(pattern);
    //给pattern的每一位对应的next数组赋值
    for (int i = 1; i < len; i++){
        k = nextarray[i-1];
        //先比较现在i位的是否和k位的相等，如果不等且k不是指向第一位数，那么
        //k-1对应的是pattern[i-1]之前对应的一位的下标，nextarray[k-1]就是上一层对应的结尾
        while (pattern[i] != pattern[k] && k != 0){
            k = nextarray[k - 1];
        }
        //如果成功匹配，赋值k+1
        if (pattern[i] == pattern[k]){
            nextarray[i] = k + 1;
        }
        //否则从头开始匹配
        else{
            nextarray[i] = 0;
        }
    }
}

void kmp(){
    int i = 0;//主串匹配到的位置
    int len = strlen(target);
    int l = strlen(pattern);
    int pos = 0;//模式串匹配到的位置
    int k = 0;//成功匹配的字符个数
    while (i < len){
        while (pattern[pos] == target[i + k]){
            pos++;
            k++;
            if (k == l){
                cout << i << endl;
                return;
            }
        }
        if (k != 0){
            i = i + (k - nextarray[k - 1]);//位移=成功匹配的长度-最后一个成功的next值
            //符合前缀的后一个开始比较
            k = nextarray[k-1];
            pos = k;
        }
        else{
            i++;
            k = 0;
            pos = 0;
        }
    }
}


int main(){
    cin >> target;
    cin >> pattern;
    setNextarray();
    kmp();
    return 0;
}

##时间复杂度 pattern处理时间是O(strlen(pattern)),匹配时间O(strlen(target))，总时间O(M+N)

sicily1282使用kmp算法

参考文档：

1.字符串模式匹配算法——BM、Horspool、Sunday、KMP、KR、AC算法一网打尽

2.KMP算法的前缀next数组最通俗的解释，如果看不懂我也没辙了

3.字符串匹配的KMP算法